Given: The graph showing the number of minutes Diane walked against the number of calories burned
To Determine: (a)how many minutes does Diane walk per calorie burned (b) the slope of the graph
Solution:
Step 1: Locate at least two points fom the graph
The points located is as shown below
So, at 10 minutes, 100 calories was burned. Also, at 20 minutes, 200 calories was burned
Therefore, the number of minutes Diane walk per calorie would be
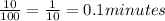
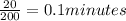
Hence, the number of minutes Diane walk per calorie burned is 0.1 minutes
(b) To Determine: The slope of the graph
The slope of a straight line graph given two points can be calculated by the formula
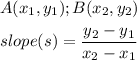
Apply the formula to find the slope of the graph from the two points selected earlier
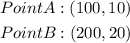
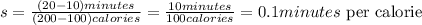
Hence
(a) The number of minutes Diane walk per calorie burned is 0.1 minutes
(b) The slope of the graph is 0.1 minutes per calorie