Question

What is the product of the complex numbers (2×i) and (3-2i)

Answer 1

Step-by-step explanation:

First, we need to know that by definition:

`i^2=-1`

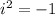
Then, to multiply the complex numbers, we can apply the distributive property as:

`2i\cdot(3-2i)=2i\cdot3-2i\cdot2i`

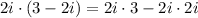
Solving the multiplication and applying the definition, we get:

`\begin{gathered} 2i\cdot(3-2i)=6i-4i^2 \\ 2i\cdot(3-2i)=6i-4(-1) \\ 2i\cdot(3-2i)=6i+4 \end{gathered}`

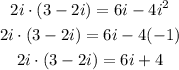
So, the product of the complex numbers is 6i + 4

Answer: 6i + 4