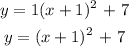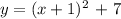
Step-by-step explanation:
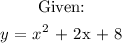
The equation of parabola in vertex form:

where (h, k) is the vertex
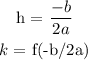
From the equation given: a = 1, b = 2, c = 8
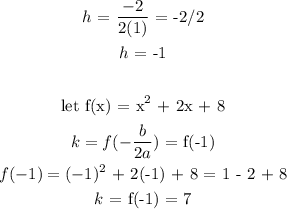
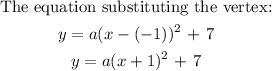
We need to find a. To get a, we will use the y-intercept.
The value of y when x = 0
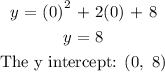
Substitute for x and y in the vertex equation using the y-intercept:
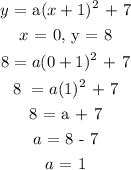
The equation in vertex form: