Question

Military rifles have a mechanism for reducing the recoil forces of the gun on the person firing it. An internal part recoils over a relatively large distance and is stopped by damping mechanisms in the gun. The larger distance reduces the average force needed to stop the internal part. (Assume the gun is fired in the positive direction.) (a) Calculate the recoil velocity (in m/s) of a 1.23 kg plunger that directly interacts with a 0.0200 kg bullet fired at 561 m/s from the gun. (Indicate the direction with the sign of your answer.) (b) If this part is stopped over a distance of 22.2 cm, what average force (in N) is exerted upon it by the gun? (Indicate the direction with the sign of your answer.) (c) Compare this to the force exerted on the gun if the bullet is accelerated to its velocity in 13.4 ms (milliseconds). (Include the sign of the value in your answer.) force on plunger by gun / force on gun by bullet =

Answer 1

We will have the following:

a)

`\begin{gathered} (0.02kg)(561m/s)=(1.23kg)v_f\Rightarrow v_f=(11.22kg\ast m/s)/(1.23kg) \\ \\ \Rightarrow v_f=(374)/(41)m/s\Rightarrow v_f\approx9.12m/s \end{gathered}`

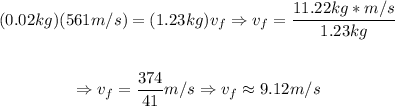
So, the recoil is approximately -9.12 m/s.

b) Now, we determine the average force of the rifle:

First, we determine the time it took to have the final velocity the bullet:

`\begin{gathered} -0.222m=(1)/(2)(0m/s-9.12m/s)t\Rightarrow t=(4551)/(93500)s \\ \\ \Rightarrow t\approx0.049s \end{gathered}`

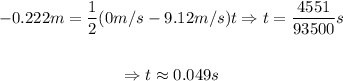
Now, we determine the average force:

`\begin{gathered} F=\frac{(1.23kg)(374/41\text{ }m/s-0m/s)}{(4551/93500s)}\Rightarrow F=230.5141727...N \\ \\ \Rightarrow F\approx230.51N \end{gathered}`

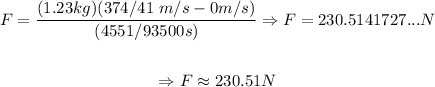
So, the average force was approximately 230.51 N.

c) If th bullet is accelerated to this velocity in 13.4 ms we will have that:

`F=((1.23kg)(374/41m/s-0m/s))/((0.0134s))\Rightarrow F\approx837.31N`

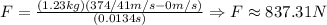
So, the force would be much greater.