We will have the following:
a)
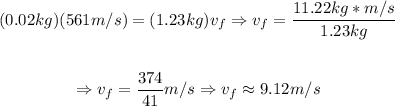
So, the recoil is approximately -9.12 m/s.
b) Now, we determine the average force of the rifle:
First, we determine the time it took to have the final velocity the bullet:
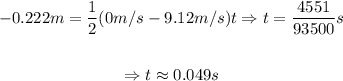
Now, we determine the average force:

So, the average force was approximately 230.51 N.
c) If th bullet is accelerated to this velocity in 13.4 ms we will have that:
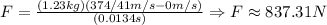
So, the force would be much greater.