To determine the maximum profit we notice that this is a quadratic function with negative leading term which means that its maximum is its vertex; if we complete the square we can find both the answers we are looking for so let's complete the squares:

Hence, we can write the function as:
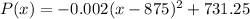
From it we notice that the vertex of the function is (875,731.25) and therefore:
• If the company sells 875 patterns the have a maximum profit.
,
• The maximum profit is $731.25