Looking at the height values, we can see that the values are being multiplied by a constant value (we have a geometric sequence).
To find the common ratio, let's divide one term by the term before.
Using bounces 2 and 1, we have:
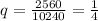
The recursive formula relates one element of the sequence with the previous element,
Since each value in the table is 4 times less than the value before, we can write the recursive formula below:
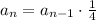
To write an explicit formula, we can use the model below:
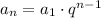
Since the first term is 10240, we have a1 = 10240, so the formula is:
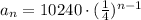
To find the height at bounce 8, let's use n = 8 and calculate the value of a8:
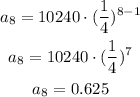
Therefore the height after bounce 8 is equal to 0.625 cm.