ANSWER
Step-by-step explanation
To solve this equation, first, square both sides of the equation,
![(\sqrt[]{25-3x})^2=(x-9)^2](https://img.qammunity.org/2023/formulas/mathematics/college/1hcgjp9sk1a3u2k9c5d7e6xs5zkqukqm2k.png)
Simplify the square root with the exponent and expand the binomial squared on the right side of the equation,
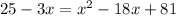
Then, subtract 25 from both sides and add 3x to both sides,
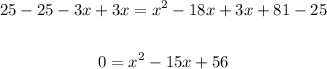
This is a quadratic equation that we can solve using the quadratic formula,
![\begin{gathered} if\text{ }ax^2+bc+c=0 \\ then\text{ }x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1eod0th1uvpaw0vtc6tkx2t3z2qxfz3n2k.png)
In this case, the coefficients are a = 1, b = -15 and c = 56,
![undefined]()