Our main objective is to describe the shaded region.
To answer this, first we need to determine the equation of the lines that bounds the shaded region.
Here we have a line at x =2 and x = 4
Notice that the shaded region is on the right of x = 2 ( therefore we can say that the shaded region is greater than x = 2 ) and on the left of x = 4 ( we can also say that the shaded region is less than x = 4
Another important thing to notice is the line that bounds the region, if it is a broken line or a solid line. If it's a broken line, it means that we dont have to include its value/expression. Instead of x is greater than or equal to 2 ( we will not include 2 since x = 2 is a broken line), we will only put it as x > 2. The same goes for the boundary at x = 4 ( being a broken line ) , it must be x < 4 only.
To further illustrate the difference, if the lines in the figure are solid lines then our answer will be:
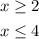
But since it's a broken line , then our answer is only:
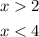
There will be times that the problem is not a vertical or horizontal line, but a slanting line. In those cases you have to solve for the equation of the lines and describe the shaded region accordingly using the concept of the broken/solid lines and > or <. If the shaded region is above or to the right of a line then use "greater than" or "greater than or equal". If the shaded region is below or to the left of the line then use " less than" or "less than or equal" as the case may be.