So we have a 60° arc defined in a 12cm radius circle. The length of an arc in a circle is equal to the product of the angle that defines it (in radians) and the radius. So the first thing we have to do is convert 60° to radians and then multiply the result by 12cm. In order to convert an angle alpha from degrees to radians we have to use the following formula:

So taking alpha equal to 60 we get:

So the 60° angle in radians is equal to π/3. Then the length of the arc is given by:
![(\pi)/(3)\cdot12\operatorname{cm}=4\pi\operatorname{cm}=12.6\operatorname{cm}]()
So the first answer is 12.6 cm.
For the second question we need to find the area of the sector defined by the arc. For an arc defined by an angle alpha in a circle with radius r the area of the sector given by the arc is equal to:
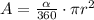
Where alpha must be written in degrees. Here alpha is equal to 60° so we get:
![\begin{gathered} A=(60)/(360)\cdot\pi\cdot(12\operatorname{cm})^2=\pi\cdot\frac{144\operatorname{cm}}{6} \\ A=\pi\cdot24\operatorname{cm}=75.4\operatorname{cm} \end{gathered}]()
Then the second answer is 75.4 cm².