Question

I have to solve this, I have option A and B, it doesn’t matter which one, I need help thxxxx

Answer 1

Lets draw a picture of the problem:

where the bearing angle is measured in a clockwise direction from the north line.

Then, we need to find the distance d_3 and the angle theta. The distances d_1 and d_2 were given as

`\begin{gathered} d_1=\text{speed x time=400mph}*2hours=800\text{ miles} \\ d_2=\text{speed x time=400mph}*3hours=1200\text{ miles} \end{gathered}`

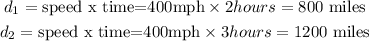
By applying the law of cosines, we have

`d^2_3=d^2_1+d^2_2-2\cdot d_1\cdot d_2\cdot\cos 80`

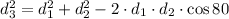
then, by substituting the given values, we get

`d^2_3=800^2_{}+1200^2-2\cdot800\cdot1200\cdot\cos 80`

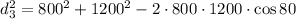
which gives

`\begin{gathered} d^2_3=640000+1440000-333404.50 \\ d^2_3=1746595.5 \end{gathered}`

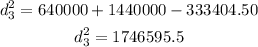
then, the distance_3 is

`\begin{gathered} d^{}_3=\sqrt[]{1746595.5} \\ d_3=1321.588 \end{gathered}`

Now, in order to obtain angle theta, we can use the law of sines as follows,

`(\sin\theta)/(d_1)=(\sin80)/(d_3)`

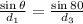
Then, we have

`\sin \theta=(\sin80)/(d_3)\cdot d_1`

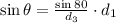
By substituting the given values, we get

`\begin{gathered} \sin \theta=(0.9848)/(1321.588)\cdot800 \\ \\ \sin \theta=0.5961 \end{gathered}`

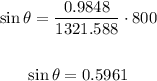
so, we obtain

`\begin{gathered} \theta=\sin ^(-1)(0.5961) \\ \theta=36.59 \end{gathered}`

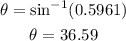
Now, lets find the bearing angle for the return flight:

From the picture, we can see that the bearing angle is 180+60 = 240 degrees.

How far is the airplane from SeaTac and what would be the bearing for the return flight?

The plane is at a distance of 1321.588 miles from the SeaTac and with a bearing angle of 240 degrees from the north line.