Lets draw a picture of the problem:
where the bearing angle is measured in a clockwise direction from the north line.
Then, we need to find the distance d_3 and the angle theta. The distances d_1 and d_2 were given as
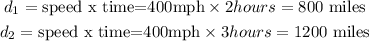
By applying the law of cosines, we have
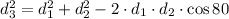
then, by substituting the given values, we get
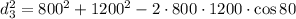
which gives
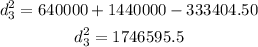
then, the distance_3 is
![\begin{gathered} d^{}_3=\sqrt[]{1746595.5} \\ d_3=1321.588 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5u1aoyec29l5lp98ilrswnotdokd95axnq.png)
Now, in order to obtain angle theta, we can use the law of sines as follows,
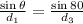
Then, we have
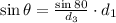
By substituting the given values, we get
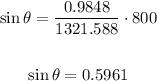
so, we obtain
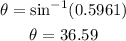
Now, lets find the bearing angle for the return flight:
From the picture, we can see that the bearing angle is 180+60 = 240 degrees.
How far is the airplane from SeaTac and what would be the bearing for the return flight?
The plane is at a distance of 1321.588 miles from the SeaTac and with a bearing angle of 240 degrees from the north line.