The binomila probabiity formula is given by

Where
p is probability of success
x is the number of trials
q is the probability of failure
n is total number of trials
To calculate the probabilities, we will use a binomial calculator. Given, p = 0.5 and n = 14. So,
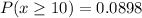
and
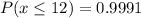
and
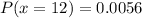
Now, the formula for the mean of a binomial distribution is
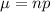
Plugging in the values, it is:
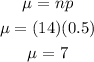
The formula for standard deviation of a binomial distribution is
![\sigma=\sqrt[]{n\cdot p\cdot(1-p)}](https://img.qammunity.org/2023/formulas/mathematics/college/49fktk68tkbphsybhcvxs6uym8ryx7kcgs.png)
Plugging in the values, we have:
![\begin{gathered} \sigma=\sqrt[]{n\cdot p\cdot(1-p)} \\ \sigma=\sqrt[]{14\cdot0.5\cdot(1-0.5)} \\ \sigma=\sqrt[]{14\cdot0.5\cdot0.5} \\ \sigma=\sqrt[]{3.5} \\ \sigma=1.8708 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1gpe5j9xrko6xdb5xpgsqnnc8xq3vwrbtd.png)