Question

Let experience a variable that possess a binomial distribution with P equals 0.5 and N equal 14 using the binomial formulation or table calculate the following probability also calculate the mean and standard deviation of the distribution around solution to 4 dustimal places

Answer 1

The binomila probabiity formula is given by

`p(x)=(n!)/((n-x)!x!)p^xq^(n-x)`

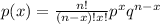
Where

p is probability of success

x is the number of trials

q is the probability of failure

n is total number of trials

To calculate the probabilities, we will use a binomial calculator. Given, p = 0.5 and n = 14. So,

`P(x\geq10)=0.0898`

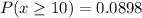
and

`P(x\leq12)=0.9991`

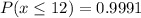
and

`P(x=12)=0.0056`

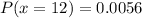
Now, the formula for the mean of a binomial distribution is

`\mu=np`

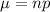
Plugging in the values, it is:

`\begin{gathered} \mu=np \\ \mu=(14)(0.5) \\ \mu=7 \end{gathered}`

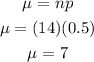
The formula for standard deviation of a binomial distribution is

`\sigma=\sqrt[]{n\cdot p\cdot(1-p)}`

Plugging in the values, we have:

`\begin{gathered} \sigma=\sqrt[]{n\cdot p\cdot(1-p)} \\ \sigma=\sqrt[]{14\cdot0.5\cdot(1-0.5)} \\ \sigma=\sqrt[]{14\cdot0.5\cdot0.5} \\ \sigma=\sqrt[]{3.5} \\ \sigma=1.8708 \end{gathered}`