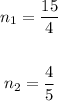Question

Find a number such that the sum and three times its reciprocal is 91/20.

Answer 1

0.8 and 3.75.

Explanation:

If the number is x, then:-

x + 3 * 1/x = 91/20

x^2 + 3 = 91x/20

x^2 - (91/20)x + 3 = 0

x^2 - 4.55x + 3 = 0

x = [-(-4.55) +/- sqrt((-4.55)^2 - 4*1*3)] / 2

x = 0.8, 3.75.

Answer 2

For this exercise you need to remember the following:

1. The sum is the result of an Addition.

2. By definition, given:

`(a)/(b)`

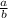
Its reciprocal is:

`=(b)/(a)`

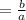
3. The word "times" indicates a Multiplication.

In this case, let be "n" the number mentioned in the exercise. Its reciprocal is:

`(1)/(n)`

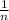
Based on the information given in the exercise, you can set up the following equation:

`n+3((1)/(n))=(91)/(20)`

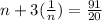
Now you must solve for "n":

1. Simplify:

`\begin{gathered} n+(3)/(n)=(91)/(20) \\ \\ ((n)(n)+3)/(n)=(91)/(20) \\ \\ (n^2+3)/(n)=(91)/(20) \\ \\ n^2+3=(91)/(20)n \end{gathered}`

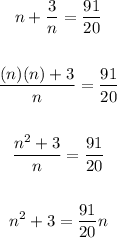
2. Make the equation equal to zero:

`n^2-(91)/(20)n+3=0`

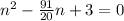
3. Apply the Quadratic formula. This is:

`n=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this case:

`\begin{gathered} a=1 \\ b=-(91)/(20)_{} \\ \\ c=3 \end{gathered}`

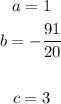
Substituting values and evaluating, you get:

`\begin{gathered} n=\frac{-(-(91)/(20))\pm\sqrt[]{(-(91)/(20))^2-2(1)(3)}}{2\cdot1} \\ \\ n_1=(15)/(4) \\ \\ n_2=(4)/(5) \end{gathered}`

The answer

There are two numbers:

`\begin{gathered} n_1=(15)/(4) \\ \\ n_2=(4)/(5) \end{gathered}`