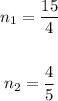For this exercise you need to remember the following:
1. The sum is the result of an Addition.
2. By definition, given:
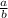
Its reciprocal is:
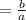
3. The word "times" indicates a Multiplication.
In this case, let be "n" the number mentioned in the exercise. Its reciprocal is:
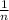
Based on the information given in the exercise, you can set up the following equation:

Now you must solve for "n":
1. Simplify:
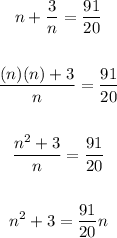
2. Make the equation equal to zero:

3. Apply the Quadratic formula. This is:
![n=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/high-school/mhwjj28st6y65qw9auy0fcdp6q6kcgffx9.png)
In this case:
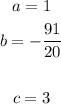
Substituting values and evaluating, you get:
![\begin{gathered} n=\frac{-(-(91)/(20))\pm\sqrt[]{(-(91)/(20))^2-2(1)(3)}}{2\cdot1} \\ \\ n_1=(15)/(4) \\ \\ n_2=(4)/(5) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/v3n8vu0r1dl6oyndtaa7lswqjqu94dmj0d.png)
The answer
There are two numbers: