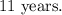Question

A principal of $2900 is invested at 3% interest, compounded annually. How many years will it take to accumulate $4000 or more in the account? (Use the calculator provided if necessary.)Write the smallest possible whole number answer.

Answer 1

To solve this problem, we will use the following formula for annually compounded interest:

`A=P(1+r)^t,`

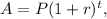
where r is the rate of interest in decimal form, t is the number of years, and P is the initial amount.

Substituting P=2900, A=4000, r=0.03 in the formula, we get:

`\begin{gathered} 4000=2900(1+0.03)^t=2900(1.03)^t, \\ (4000)/(2900)=1.03^t. \end{gathered}`

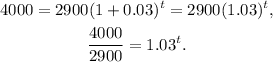
Applying log to both sides of the equation we get:

`log((40)/(29))=tlog1.03.`

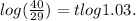
Therefore:

`t=(log(40)/(29))/(log1.03)\approx10.88\text{ years.}`

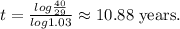
Rounding the smallest possible whole number, we get:

`t=11\text{ years.}`

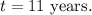
Answer:

`11\text{ years.}`