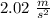 Step-by-step explanation
Step-by-step explanationStep 1
Free body diagram
Step 2
Newton's second law says that when a constant force acts on a massive body, it causes it to accelerate, a force applied to an object at rest causes it to accelerate in the direction of the force.it is given by the formula
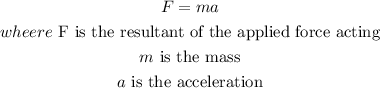
so
a)let
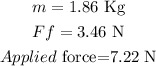
b) now ,replace and solve for a
from the free body diagram and the data we know that the object accelerates horizontally ,so the sum of the applied force make the object moves rigthwards
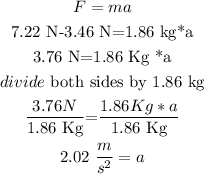
therefore,
the acceleration of the objects is 2.02 meters per square second
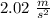
I hope this helps you