Question

Are [2/3 9/13] and [-13/3 9/-2] inverses? why or why not?

Answer 1

Given:- The matrix:

`\begin{bmatrix}{2} & {9} \\ {3} & {13}\end{bmatrix},\begin{bmatrix}{-13} & {9} \\ {3} & {-2}\end{bmatrix}`

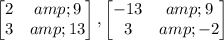
To check the given matrix are inverse.

Solution:-

As we know that when the two matrices are inverse then their resultant is equal to the identity matrix I.

So, multiplying the given matrices as:

`\begin{gathered} \begin{bmatrix}{2} & {9} \\ {3} & {13}\end{bmatrix}\begin{bmatrix}{-13} & {9} \\ {3} & {-2}\end{bmatrix}=\begin{bmatrix}{2*(-13)}+9*3 & {2*9}+9*(-2) \\ {3*(-13)+13*3} & {3*9+13*(-2)}\end{bmatrix} \\ \begin{bmatrix}{2} & {9} \\ {3} & {13}\end{bmatrix}\begin{bmatrix}{-13} & {9} \\ {3} & {-2}\end{bmatrix}=\begin{bmatrix}{-26+27} & {18-18} \\ {-39+39} & {27-26}\end{bmatrix} \\ \begin{bmatrix}{2} & {9} \\ {3} & {13}\end{bmatrix}\begin{bmatrix}{-13} & {9} \\ {3} & {-2}\end{bmatrix}=\begin{bmatrix}{1} & {0} \\ {0} & {1}\end{bmatrix} \end{gathered}`

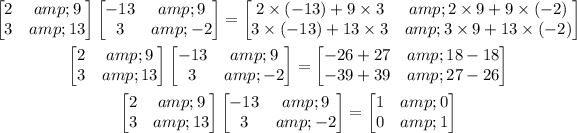
As we can observe that the resultant of the two matrix multiplication is an Identity matrix.

So, the given matrices are inverse.

Final answer:-

Therefore, the given matrices are inverse of each other.

Option (C) is correct.