Given:- The matrix:
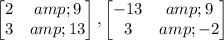
To check the given matrix are inverse.
Solution:-
As we know that when the two matrices are inverse then their resultant is equal to the identity matrix I.
So, multiplying the given matrices as:
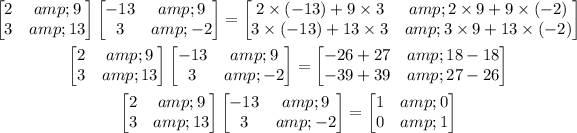
As we can observe that the resultant of the two matrix multiplication is an Identity matrix.
So, the given matrices are inverse.
Final answer:-
Therefore, the given matrices are inverse of each other.
Option (C) is correct.