We need to find the probability of exactly three successes in six trials of a binomial experiment. Probability of success 50% (no success is 50%).
To find this probability, we need to use the following formula for Bernoulli Trials (or Binomial Experiment):
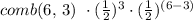
The combinations are given by:
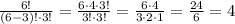
Then, we have:
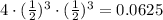
Thus, the probability of exactly three successes in six trials of a binomial experiment (which the probability of success is 50%) is 0.0625.
Rounding to the nearest tenth is about p = 0.1 (1/10) or 10%.