Solution:
The area of the shape is the sum of the areas of the triangles ABE and BCD as shown below:
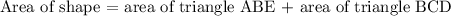
Area of triangle ABE:
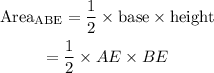
To evalutae the area of triangle ABE, we need the dimensions of the triangle ABE.
AE: To evaluate AE, we determine the distance between the points A and E.
Where the respective coordinates of A and E are (-4,0) and (0,0).
The distance between any two points is expressed as
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are the endpoints of the line} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/g6nul9vhn2n3sbgnwrwsqqtvspoxmgn1qr.png)
Thus, the distance AE is evaluated as
![\begin{gathered} AE=\sqrt[]{(0_{}-(-4)_{})^2+(0-0)^2} \\ \Rightarrow\sqrt[]{16} \\ \therefore AE=4\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/65d5z8zwyvuutwiw9bykbz5llw5hjkg9ay.png)
similarly, BE has endpoints B and E whose respective coordinates are (0,4) and (0,0).
Thus,
![\begin{gathered} BE=\sqrt[]{(0_{}-0_{})^2+(0-4)^2} \\ \Rightarrow\sqrt[]{16} \\ \therefore BE=4\text{ units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/k2vk9c1tt1s8erf243eae33azhd6n8z21c.png)
Hence, the area of the triangle ABE becomes
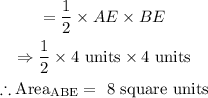
Area of triangle BCD:
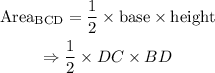
DC has endpoints at D and C whose respective coordinates are (0,2) and (2,2).
Thus,
![\begin{gathered} DC=\sqrt[]{(2-0)^2+(2-2)^2} \\ =\sqrt[]{4} \\ \Rightarrow DC\text{ = 2 units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kthm9bx86o6rroedvel6f560ipzu1xg5fe.png)
BD has endpoints at B and D whose respective coordinates are (0,4) and (0,2).
Thus,
![\begin{gathered} BD=\sqrt[]{(0-0)^2+(2-4)^2} \\ =\sqrt[]{4} \\ \Rightarrow BD=\text{ 2 units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7p86rc9merz51xmph1o036yxsmh7xjcxq0.png)
Hence, area of the triangle BCD becomes
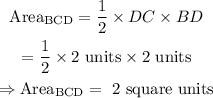
Recall that:
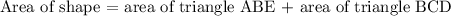
Thus,
.