Question

What is the slope of a line perpendicular to the line whose equation is 10x-8y= -80.Fully simplify your answer.

Answer 1

We are given the following line equation:

`10x-8y=-80`

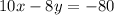
We are asked to determine the slope of the line perpendicular to the given line, to do that we need to have into account that two lines are perpendicular when the following relationship between their slopes is true:

`m_1=-(1)/(m_2)`

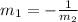
Where:

`m_1,m_2=\text{ slopes of the lines. }`

Therefore, we need to determine the slope of the given lines. To do that we will convert the given equation into the slope-intercept form, this means:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept. To do that we will solve for "y", first by subtracting "10x" from both sides:

`-8y=-80-10x`

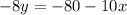
Now we divide both sides by -8:

`y=-(80)/(-8)-(10)/(-8)x`

Solving the operations:

`y=10+(5)/(4)x`

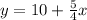
Therefore, the slope of the given line is:

`m_2=(5)/(4)`

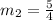
Now we use the relationship between slopes to determine the slope of the perpendicular line:

`m_1=-(1)/((5)/(4))=-(4)/(5)`

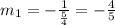
Therefore, the slope of the perpendicular line is -4/5.