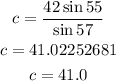At first, let us find the measure of angle B
The sum of angles of a triangle is 180 degrees
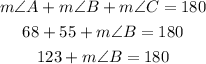
Subtract 123 from both sides to fin m < B
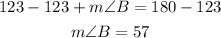
Now, let us use the sin rule
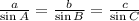
Since b = 42, then
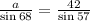
By using cross multiplication
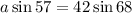
Divide both sides by sin 57
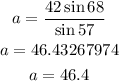
Do the same to find c
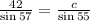
By using cross multiplication
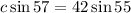
Divide both sides by sin 57