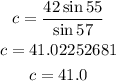Question

Consider a triangle ABC like the one below. Suppose that A=68°, C = 55°, and b= 42. (The figure is not drawn to scale.) Solve the triangle. Round your answers to the nearest tenth. If there is more than one solution, use the button labeled "or". E E B 12 c T B = 57°, a = = 0,c=0 No solution X Х 6 ?

Answer 1

At first, let us find the measure of angle B

The sum of angles of a triangle is 180 degrees

`\begin{gathered} m\angle A+m\angle B+m\angle C=180 \\ 68+55+m\angle B=180 \\ 123+m\angle B=180 \end{gathered}`

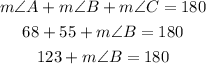
Subtract 123 from both sides to fin m < B

`\begin{gathered} 123-123+m\angle B=180-123 \\ m\angle B=57 \end{gathered}`

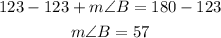
Now, let us use the sin rule

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

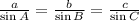
Since b = 42, then

`(a)/(\sin68)=(42)/(\sin 57)`

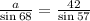
By using cross multiplication

`a\sin 57=42\sin 68`

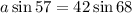
Divide both sides by sin 57

`\begin{gathered} a=(42\sin 68)/(\sin 57) \\ a=46.43267974 \\ a=46.4 \end{gathered}`

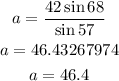
Do the same to find c

`(42)/(\sin57)=(c)/(\sin 55)`

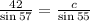
By using cross multiplication

`c\sin 57=42\sin 55`

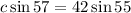
Divide both sides by sin 57

`\begin{gathered} c=(42\sin 55)/(\sin 57) \\ c=41.02252681 \\ c=41.0 \end{gathered}`