Given,
The mass of the car is m
The intial velocity of the car is v
From the law of conservation of momentum, the momentum of the system remains constant.
Thus,
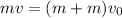
Where v₀ is the velocity of the two cars that are stuck together after the collision.
On simplifying,

The kinetic energy before the collision is,
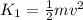
The kinetic energy before the collision is,
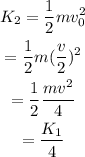
Thus the kinetic energy of the system after the collision is one-fourth as much as before.
Threfore, the correct answer is option A.