Answer:
y = 72.35 + 2.95x
Explanations:
Let the number of tutorials attended be represented by x
Let the semester grade be represented by y
x = { 9, 4, 0, 0, 6, 1}
y = {99, 91, 63, 78, 85, 77}
Calculate the mean of x
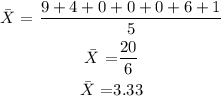
Calculate the mean of y

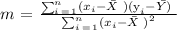
![\begin{gathered} m\text{ = }((9-3.33)(99-82.17)+(4-3.33)(91-82.17)+(0-3.33)(63-82.17)+(0-3.33)(78-82.17)+(6-3.33)(85-82.17)+(1-3.33)(77-82.17))/(\mleft(9-3.33\mright)^2+\mleft(4-3.33\mright)^2+(0-3.33)^2+(0-3.33)^2+(6-3.33)^2+(1-3.33)^2) \\ \text{m = }\frac{198.67}{^{}67.33} \\ \text{m = }2.95 \end{gathered}]()
Calculate the y-intercept using the formula below:
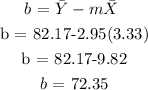
The equation of a line is:
y = mx + b
Substitute m = 2.95 and b = 72.35 into the equation of a line given above:
y = 2.95x + 72.35