Question

Which of the following expressions is not equal to 1? explain your reasoning!

Answer 1

Let's simplify each expression shown in the exercise:

Option a

Given:

`x^3\cdot x^(-3)`

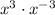
You can apply the Product of powers property. This states the following:

`b^n\cdot b^m=b^((n+m))`

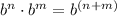
Where "b" is the base and "n" and "m" are exponents.

Then, you get:

`x^3\cdot x^(-3)=x^((3+(-3)))=x^((3-3))=x^0`

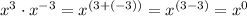
By definition:

`b^0=1`

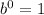
Therefore:

`x^0=1`

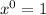
The expression given in Option a is equal to 1.

Option b

Knowing that any number or expression with exponent zero is equal to 1, you get that:

`1001^0=1`

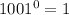
The expression given in Option b is equal to 1.

Option c

Given:

`(a^2b)/(ba^2)`

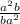
You can notice that the numerator and the denominator are equal, then:

`(a^2b)/(ba^2)=1`

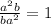
The expression given in Option c is equal to 1.

Option d

Given:

`(y^2)/(y^(-2))`

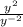
You can simplify it using the Quotient of powers property, which states that:

`(b^m)/(b^n)=b^((m-n))`

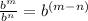
Then, you get:

`y^((2-(-2)))=y^((2+2))=y^4`

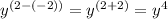
The expression given in Option d is not equal to 1.

The answer is: Option d.