Question

Using the completing the square method solve for 4x squared minus 8x minus 5 equal to 04x² - 8x - 5 = 0

Answer 1

x = -1/2 and x = 5/2

Step-by-step explanation

The method of completing the square consists of rewriting a quadratic equation as a binomial squared,

`(a\pm b)^2=a^2\pm2ab+b^2`

First, we have to identify the first term, a. Note that in the given equation, we have 4x², and 4 is 2², so this term is equivalent to,

`4x^2=(2x)^2`

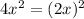
Therefore, our first term is 2x.

Then, we have to find the second term, b. In the given equation, the second term is -8x, which is equal to 2ab in the binomial squared rule. We know that a = 2x, so now we can find b,

`\begin{gathered} 2ab=-8x \\ \\ 2\cdot2x\cdot b=-8x \end{gathered}`

Solving for b,

`\begin{gathered} 4xb=-8x \\ \\ b=(-8x)/(4x)=-2 \end{gathered}`

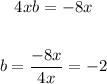
Now, write the binomial and expand it with the rule stated at the top of the Explanation section,

`(2x-2)^2=4x^2-8x+4`

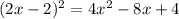
The result is not equal to the given equation, so, to be able to replace the first two terms of the equation for this binomial squared, we have to add 4 to both sides of the equation,

`\begin{gathered} 4x^2-8x+4-5=0+4 \\ \\ (2x-2)^2-5=4 \end{gathered}`

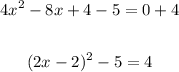
Finally, we have to solve for x. First, add 5 to both sides,

`\begin{gathered} (2x-2)^2-5+5=4+5 \\ \\ (2x-2)^2=9 \end{gathered}`

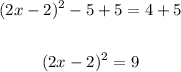
Then, take the square root of both sides,

`\begin{gathered} √((2x-2)^2)=\pm√(9) \\ \\ 2x-2=\pm3 \end{gathered}`

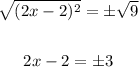
Add 2 to both sides,

`\begin{gathered} 2x-2+2=2\pm3 \\ \\ 2x=2\pm3 \end{gathered}`

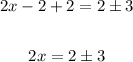
And then, divide both sides by 2,

`x=(2\pm3)/(2)`

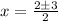
So, we have the two solutions,

`\begin{gathered} x_1=(2+3)/(2)=(5)/(2) \\ \\ x_2=(2-3)/(2)=-(1)/(2) \end{gathered}`

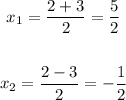
Hence, the two solutions are x = -1/2 and x = 5/2.