ANSWER
x = -1/2 and x = 5/2
Step-by-step explanation
The method of completing the square consists of rewriting a quadratic equation as a binomial squared,
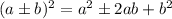
First, we have to identify the first term, a. Note that in the given equation, we have 4x², and 4 is 2², so this term is equivalent to,
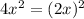
Therefore, our first term is 2x.
Then, we have to find the second term, b. In the given equation, the second term is -8x, which is equal to 2ab in the binomial squared rule. We know that a = 2x, so now we can find b,
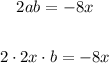
Solving for b,
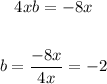
Now, write the binomial and expand it with the rule stated at the top of the Explanation section,
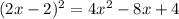
The result is not equal to the given equation, so, to be able to replace the first two terms of the equation for this binomial squared, we have to add 4 to both sides of the equation,
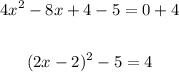
Finally, we have to solve for x. First, add 5 to both sides,
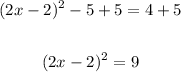
Then, take the square root of both sides,
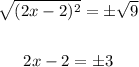
Add 2 to both sides,
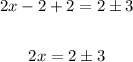
And then, divide both sides by 2,
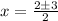
So, we have the two solutions,
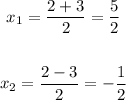
Hence, the two solutions are x = -1/2 and x = 5/2.