1) Let's tackle this question by dividing it into two parts.
2) SAT
Note that given that the student gets a score in the 59 percentile, we need to find the corresponding z-score for a probability of 0.59. Resorting to a standard normal table, we can state that:
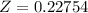
Now, let's find the raw score plugging into that the z-score into the Z score formula:
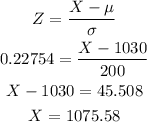
We still need to round it off to the nearest whole number: 1076
3) ACT
The process will be very similar to the previous one, so let's find the ACT score, considering that