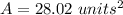Given the following vertices of the triangle ABC:
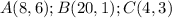
You can plot them on a Coordinate plane and Adraw the triangle. See the picture below:
You need to find the lengths AB, BC and AC. To do this, you can use the formula for calculate the distance between two points:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2_{}}](https://img.qammunity.org/2023/formulas/mathematics/college/dzmv1rerjpvrh7y9ed9nd93i81hhwfhy06.png)
Then, substituting the corresponding coordinates into the formula and evaluating, you get:
![\begin{gathered} AB=\sqrt[]{(20-8)^2+(1-6)^2}=13\text{ }units \\ \\ \\ BC=\sqrt[]{(4-20)^2+(3-1)^2}=2\sqrt[]{65}\text{ }units \\ \\ \\ AC=\sqrt[]{(4-8)^2+(3-6)^2}=5\text{ }units \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/b87xhabkpvtiyj9i5rq71g0z59wqye9c4k.png)
You know that you can calculate the area using Heron's formula:
![A=\sqrt[]{s(s-a)(s-b)(s-c)}](https://img.qammunity.org/2023/formulas/mathematics/college/t3rmhsk71nltcmgtu237bvtgrmrx89v4xv.png)
Where "a", "b" and "c" are the lengths of the sides of the triangle and "s" is the semiperimeter.
Then, you can find the value of "s" as following:
![\begin{gathered} s=\frac{13\text{ }units+2\sqrt[]{65}\text{ }units+5\text{ }units}{2} \\ \\ s\approx17.06\text{ }units \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/83bbkcp11znvjzx8majytnvhwfg5a0cf2u.png)
Knowing that:
![\begin{gathered} a=AB=13\text{ }units \\ b=BC=2\sqrt[]{65}\text{ }units\approx16.12\text{ }units \\ c=AC=5\text{ }units \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zfgcao16dtb47w0zpljio5zk5tzqsychoz.png)
You can substitute values into the formula and then evaluate, in order to find the area of the triangle:
![\begin{gathered} A=\sqrt[]{s(s-a)(s-b)(s-c)} \\ A=\sqrt[]{(17.06\text{ }units)(17.06\text{ }units-13units)(17.06\text{ }units-16.12\text{ }units)(17.06\text{ }units-5units)} \\ A=28.02\text{ }units^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h3yw9f2kzjuwc52qu68lg745sda1379ltm.png)
The answer is: