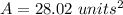Question

Find the area of a triangle with vertices A(8,6) B(20,1) and C (4,3)

Answer 1

Given the following vertices of the triangle ABC:

`A\mleft(8,6\mright);B\mleft(20,1\mright);C\mleft(4,3\mright)`

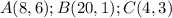
You can plot them on a Coordinate plane and Adraw the triangle. See the picture below:

You need to find the lengths AB, BC and AC. To do this, you can use the formula for calculate the distance between two points:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2_{}}`

Then, substituting the corresponding coordinates into the formula and evaluating, you get:

`\begin{gathered} AB=\sqrt[]{(20-8)^2+(1-6)^2}=13\text{ }units \\ \\ \\ BC=\sqrt[]{(4-20)^2+(3-1)^2}=2\sqrt[]{65}\text{ }units \\ \\ \\ AC=\sqrt[]{(4-8)^2+(3-6)^2}=5\text{ }units \end{gathered}`

You know that you can calculate the area using Heron's formula:

`A=\sqrt[]{s(s-a)(s-b)(s-c)}`

Where "a", "b" and "c" are the lengths of the sides of the triangle and "s" is the semiperimeter.

Then, you can find the value of "s" as following:

`\begin{gathered} s=\frac{13\text{ }units+2\sqrt[]{65}\text{ }units+5\text{ }units}{2} \\ \\ s\approx17.06\text{ }units \end{gathered}`

Knowing that:

`\begin{gathered} a=AB=13\text{ }units \\ b=BC=2\sqrt[]{65}\text{ }units\approx16.12\text{ }units \\ c=AC=5\text{ }units \end{gathered}`

You can substitute values into the formula and then evaluate, in order to find the area of the triangle:

`\begin{gathered} A=\sqrt[]{s(s-a)(s-b)(s-c)} \\ A=\sqrt[]{(17.06\text{ }units)(17.06\text{ }units-13units)(17.06\text{ }units-16.12\text{ }units)(17.06\text{ }units-5units)} \\ A=28.02\text{ }units^2 \end{gathered}`

The answer is:

`A=28.02\text{ }units^2`