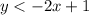Question

Write an inequality that contains the given points in its solution. I tried the first one but I’m not sure if that is what’s it’s asking…

Answer 1

For the inequality, the line defines the boundary of the region that is shaded. This indicates that any ordered pair in the shaded region, including the boundary line, will satisfy the inequality. To see that this is the case, choose a few test points and substitute them into the inequality.

(A) When x = 0 , y = 0

`\begin{gathered} y=-2x+1 \\ 0=-2(0)+1 \\ 0\\e1 \\ 0<1 \\ y<-2x+1 \end{gathered}`

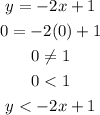
(B) When x = -5 , y = 1

`\begin{gathered} y=-2x+1 \\ 1=-2(-5)+1 \\ 1=10+1 \\ 1\\e11 \\ 1<11 \\ y<-2x+1 \end{gathered}`

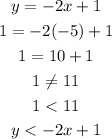
Therefore the inequality =

`y<-2x+1`