Step-by-step explanation
If two triangles are similar to each other then they have the same shape i.e. they have the same angles. Using this and the fact that the sum of the three internal angles of a triangle is always 180° we can check which pair of triangles are similar. So we can start by using the later property to find the angles of all the triangles.
We begin with triangle DEF. The sum of its angles is:
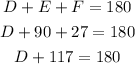
We can substract 117 from both sides:
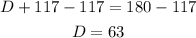
So its angles are 27°, 63° and 90°.
Then we continue with triangle GHI:
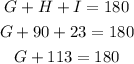
We can substract 113 from both sides:
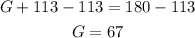
So its angles are 23°, 67° and 90°.
Then we have triangle ABC:
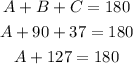
We substract 127 from both sides:
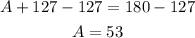
So its angles are 37°, 53° and 90°.
Then we have triangle JKL:
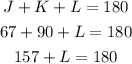
Then we substract 157 from both sides:
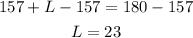
So its angles are 23°, 67° and 90°.
As you can see there's only one pair of triangles with the same angles: GHI and JKL.
Answer
Then the answer is option C.