Question

From the top of a lighthouse 130ft above sea level the measure of the angle of depression is 40 degrees. Find, to the nearest tenth, the distance from the boat to the foot of the lighthouse.

Answer 1

The distance between the boat and the base of the lighthouse, the height of the lighthouse, and the distance between the top of the lighthouse and the boat form a right triangle.

The angle of depression (marked green in the sketch above) and the top inner angle of the triangle (θ) are complementary angles, which means that they add up to 90º, so that:

`40+\theta=90`

From this expression, we can determine the measure of the angle:

`\begin{gathered} \theta=90-40 \\ \theta=50 \end{gathered}`

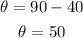
Now that we know the measure on the angle, we can use the trigonometric ratios to calculate the measure of the missing side. The trigonometric ratio that relates the opposite and adjacents sides of a right triangle with one of its angles is the tangent, defined as:

`\tan \theta=\frac{\text{opposite}}{\text{hypothenuse}}`

The "opposite" side to the angle θ is the distance between the boat and the bottom of the lighthouse and the "adjacent" side to the angle θ is the height of the lighthouse.

Then:

`\tan 50=(x)/(130)`

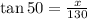
To determine the value of x, multiply both sides of the expression by 130:

`\begin{gathered} 130\cdot\tan 50=130\cdot(x)/(130) \\ 130\cdot\tan 50=x \\ x=154.927 \\ x\approx154.9ft \end{gathered}`

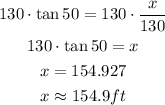
The distance from the boat to the foot of the lighthouse is 154.9ft