Let r be the radius (in cm) of the barrel, and h be its height (in cm), then we can set the following equations:
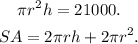
Solving the first equation for h we get:
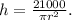
Substituting the above equation in the second equation we get:
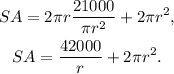
Now, we will use the first and second derivative criteria to obtain the minimum value for the above equation for the Surface Area.
The first and second derivatives of SA are:
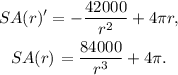
Setting SA(r)'=0 and solving for r we get:

Evaluating SA''(r) at r=14.95 we get:
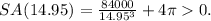
Therefore, SA(r) reaches a local minimum at r≈15.0.
Substituting r=15.0 in h(r) we get:
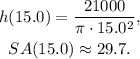
Answer: The radius is 15.0 cm and the height is 29.7 cm.