Question

What is the asymptote of the graph f(x) = 5^x - 1

Answer 1

Step-by-step explanation

The asymptote of the graph

`f\mleft(x\mright)=5^x-1`

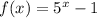
can be seen below.

Horizontal Asymptote

Line y=L is a horizontal asymptote of the function y=f(x), if either

`lim_(x→∞)f\mleft(x\mright)=L\text{ }or\text{ }lim_(x→−∞)f\mleft(x\mright)=L,and\text{ }L\text{ }is\text{ }finite.`

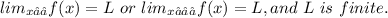
Therefore,

`\begin{gathered} \lim_(x\to+\infty\:)\left(5^x-1\right)=\infty \\ \lim_(x\to-\infty\:)\left(5^x-1\right)=-1 \end{gathered}`

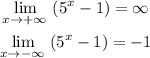
Answer: Thus, the horizontal asymptote is y = −1.

Vertical Asymptote

The line x=L is a vertical asymptote of the function y=5^x−1, if the limit of the function (one-sided) at this point is infinite.

In other words, it means that possible points are points where the denominator equals 0 or doesn't exist.

So, find the points where the denominator equals 0 and check them.

As can be seen, there are no such points, so this function doesn't have vertical asymptotes

Answer: No vertical asymptote