We are given the following information:
y varies directly as x and inversely as the square of z
y = 40 when x = 64 and z = 4
We are asked to find the value of y when x = 2 and z = 6.
To answer this, we must first express the relationship of x, y, and z:
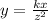
In the equation above, k is the constant of variation.
We placed x in the numerator as it varies directly as y, meaning, when y increases, x also increases and vice versa.
Meanwhile, z^2 is in the denominator because it varies inversely as y--when y increases, z^2 decreases and vice versa.
Now that we have an equation to work with, we can use the given values of x, y, and z to solve for k.

Now that we know the value of k, we can solve for y when x =2 and z = 6 using the same equation.
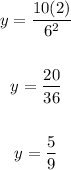
The answer is 5/9.