Question

I need help with this question please. This is non graded.

Answer 1

Given:

vertex : (-5, -10)

Point : (0, 15)

A quadratic equation can be written in its vertex form as:

`f(x)=a(x−h)^2+k`

Where (h,k) is the coordinate of the vertex and a is the constant multiplier

For this problem,

`(h,\text{ k\rparen = \lparen-5, -10\rparen}`

Hence, we can write:

`\begin{gathered} f(x)\text{ = a\lparen x-\lparen-5\rparen\rparen}^2\text{ - 10} \\ f(x)=\text{ a\lparen x + 5\rparen}^2\text{ - 10} \end{gathered}`

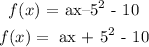
Since the point (0, 15) lies on the curve, we can substitute and solve for a:

`\begin{gathered} 15\text{ = a\lparen0+ 5\rparen}^2\text{ - 10} \\ 15\text{ = 25a - 10} \\ 25a\text{ = 15 + 10} \\ 25a\text{ = 25} \\ Divide\text{ both sides by 25} \\ (25a)/(25)\text{ = }(25)/(25) \\ a\text{ = 1} \end{gathered}`

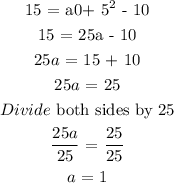
Hence, in vertex form, the quadratic equation is:

`y\text{ = \lparen x + 5\rparen}^2\text{ - 10}`

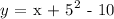
Answer: Option C