In order to graph this inequality, first let's define some ordered pairs:
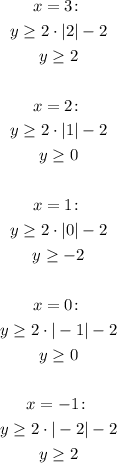
Now, graphing these points and filling the region above the lines, we have:
Looking at the options, the point that is inside this region is the point (1, 0), therefore the correct option is the third one.