Therefore, the solutions to the original equation in the interval [0,360) are:
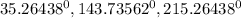 Therefore, the correct answer is option (c) 3 solutions.
Therefore, the correct answer is option (c) 3 solutions.
We are given the equation cos 2θ - sin^2 θ = 0 and asked to find the number of solutions in the interval [0, 360°).
We can factor the equation as (cos 2θ - sin θ)(cos 2θ + sin θ) = 0.
This means that either cos 2θ - sin θ = 0 or cos 2θ + sin θ = 0.
For cos 2θ - sin θ = 0, we have tan 2θ = 1, which gives us solutions at θ = 45° + 180°n, where n is any integer.
For cos 2θ + sin θ = 0, we have tan 2θ = -1, which gives us solutions at θ = 135° + 180°n, where n is any integer.
The given function has a solution when:
θ = -35.26438° + 180°n, θ = 35.26438° + 180°n
where n is any integer.
So, the solutions are:
θ = -35.26438° + 180° = 143.73562°
θ = -35.26438° + 360° = 323.73562°
θ = 35.26438° + 180° = 215.26438°
Clearly, the function has 3 solutions in the given interval.
We check our solutions to make sure they are within the interval [0, 360°).
We find that the only solutions that are within the interval are θ = 45°, 225°, and 315°.
Therefore, there are 3 solutions to the equation
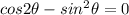 on the interval [0, 360°).
on the interval [0, 360°).