Question

Vector u has an initial point at (−5, 2) and a terminal point at (−7, 9). Which of the following represents u in trigonometric form?

Answer 1

2nd option

`u=7.28\cdot(\cos 105.945\degree i+\sin 105.945\degree j)`

Explanation:

We have that the trigonometric form is as follows:

`u=|u|\cdot(\cos \theta i+\sin \theta j)`

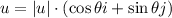
The first thing is to calculate the normal of the vector u, which would be the distance between both points, like this:

`\begin{gathered} |u|=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)_{}}^2 \\ \text{ we replacing} \\ |u|=\sqrt[]{(-7-(-5))^2+(9-2)^2_{}} \\ |u|=\sqrt[]{(-7+5)^2+(7_{})^2_{}}^{}=\sqrt[]{2^2+7^2}=\sqrt[]{4+49}=\sqrt[]{53} \\ |u|=7.28 \end{gathered}`

Now, the angle is calculated as follows:

`\begin{gathered} \tan \theta=(y)/(x) \\ \text{ in this case:} \\ \tan \theta=(y_2-y_1)/(x_2-x_1)=(9-2)/(-7-(-5))=(7)/(-7+5)=-(7)/(2) \\ \tan \theta=-(7)/(2) \\ \theta=\arctan \mleft(-(7)/(2)\mright) \\ \theta=-74.055\degree \\ \theta=-74.055\degree+180\degree \\ \theta=105.945\degree \end{gathered}`

Therefore, the vector u in its trigonometric form would be:

`u=7.28\cdot(\cos 105.945\degree i+\sin 105.945\degree j)`