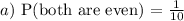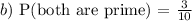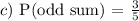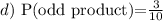Given the numbers:
{1,2,3,4,5}
If two numbers are randomly selected without replacement, let's find the following:
a) Both are even
Number of even numbers in {1,2,3,4,5} = 2 and 4 = two even numbers.
Probability that even numbers are picked without replacement is:


b) Both are prime:
Number of prime numbers in {1,2,3,4,5} = 1, 3 and 5 = three prime numbers
Probability that the random umbers picked are prime numbers is:
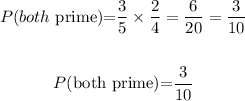
c) The sum of the numbers is odd.
we have the following:
1 + 2
1 + 4
2 + 3
2 + 5
3 + 4
4 + 5
Here, we have 6 possible sets where the sum of the numbers is odd.
Total number of sets using =

Thus, we have:
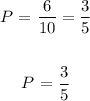
d) The product of the numbers is odd:
1 x 3
1 x 5
3 x 5
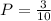
ANSWER: