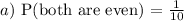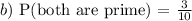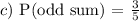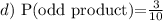Question

Twonumbersarerandomlyselectedwithoutreplacementfrom{1,2,3,4,5}.Findtheprobabilitythat:a) Bothareeven.b) Bothareprime.c) Thesumofthe numbersis odd.d) Theproductofthenumbersis odd.

Answer 1

Given the numbers:

{1,2,3,4,5}

If two numbers are randomly selected without replacement, let's find the following:

a) Both are even

Number of even numbers in {1,2,3,4,5} = 2 and 4 = two even numbers.

Probability that even numbers are picked without replacement is:

`P(\text{even)}=(2)/(5)*(1)/(4)=(2)/(20)\text{ = }(1)/(10)`
`P(\text{even)}=(1)/(10)`

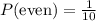
b) Both are prime:

Number of prime numbers in {1,2,3,4,5} = 1, 3 and 5 = three prime numbers

Probability that the random umbers picked are prime numbers is:

`\begin{gathered} P(both\text{ prime)=}(3)/(5)*(2)/(4)=(6)/(20)=(3)/(10) \\ \\ P(\text{both prime)=}(3)/(10) \end{gathered}`

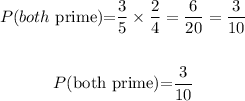
c) The sum of the numbers is odd.

we have the following:

1 + 2

1 + 4

2 + 3

2 + 5

3 + 4

4 + 5

Here, we have 6 possible sets where the sum of the numbers is odd.

Total number of sets using =

`^5C_2=(5!)/(2!(5-2)!)=(5!)/(2!(3)!)=10`

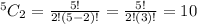
Thus, we have:

`\begin{gathered} P\text{ = }(6)/(10)=(3)/(5) \\ \\ P\text{ = }(3)/(5) \end{gathered}`

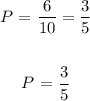
d) The product of the numbers is odd:

1 x 3

1 x 5

3 x 5

`P=(3)/(10)`

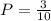
ANSWER:

`a)\text{ P(both are even) = }(1)/(10)`
`b)\text{ P(both are prime) = }(3)/(10)`
`c)\text{ P(odd sum) = }(3)/(5)`
`d)\text{ P(odd product)=}(3)/(10)`