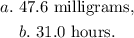Question

The drug Valium is eliminated from the bloodstream exponentially with a half-life of 36 hours. Suppose that a patient receives an initial dose of 60 milligrams of Valium at midnight.a. How much Valium is in the patient's blood at noon on the first day?b. Estimate when the Valium concentration will reach 55% of its initial level.

Answer 1

Given that the drug is eliminated exponentially, you can set the following equation:

`T=Pb^t,`

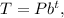
where P is the initial dose, and t is the time in hours.

To determine the value of b, you use the fact that it has a half-life time of 36 hours, therefore:

`(P)/(2)=Pb^(36).`

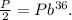
Solving for b, you get:

`\begin{gathered} (1)/(2)=b^(36), \\ b=\frac{1}{\sqrt[36]{2}}. \end{gathered}`

Therefore:

`T=P(\frac{1}{\sqrt[36]{2}})^t.`

Now, to determine the amount of Valium after 12 hours, you evaluate the expression at t=12:

`T=60(\frac{1}{\sqrt[36]{2}})^(12).`

Now, the 55% of 60 is 33, setting the equation equal to 33, and solving for t, you get:

`\begin{gathered} 33=60(\frac{1}{\sqrt[36]{2}})^t, \\ (33)/(60)=(\frac{1}{\sqrt[36]{2}})^t, \\ ln((33)/(60))=tln(\frac{1}{\sqrt[36]{2}}). \\ t=\frac{ln((33)/(60))}{ln(\frac{1}{\sqrt[36]{2}})}. \end{gathered}`

Answer:

`\begin{gathered} a.\text{ 47.6 milligrams,} \\ b.\text{ 31.0 hours.} \end{gathered}`