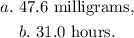Given that the drug is eliminated exponentially, you can set the following equation:

where P is the initial dose, and t is the time in hours.
To determine the value of b, you use the fact that it has a half-life time of 36 hours, therefore:
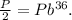
Solving for b, you get:
![\begin{gathered} (1)/(2)=b^(36), \\ b=\frac{1}{\sqrt[36]{2}}. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uchw0pvz1iyekccvw4tohphl0soylww5h6.png)
Therefore:
![T=P(\frac{1}{\sqrt[36]{2}})^t.](https://img.qammunity.org/2023/formulas/mathematics/college/3celza34bufu0735h4pxa37rzfpalutwbv.png)
Now, to determine the amount of Valium after 12 hours, you evaluate the expression at t=12:
![T=60(\frac{1}{\sqrt[36]{2}})^(12).](https://img.qammunity.org/2023/formulas/mathematics/college/ehb9tj18u0o68397rnaae77pr77dqae6qy.png)
Now, the 55% of 60 is 33, setting the equation equal to 33, and solving for t, you get:
![\begin{gathered} 33=60(\frac{1}{\sqrt[36]{2}})^t, \\ (33)/(60)=(\frac{1}{\sqrt[36]{2}})^t, \\ ln((33)/(60))=tln(\frac{1}{\sqrt[36]{2}}). \\ t=\frac{ln((33)/(60))}{ln(\frac{1}{\sqrt[36]{2}})}. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ty8ntmi8rwmrnevf731o4hzva7fnsyw2fh.png)
Answer: