We can directly remove m^12 from the square root, and stay only with 98 inside the square root
![\sqrt[]{98m^(12)}=m^{(12)/(2)}\sqrt[]{98}=m^6\sqrt[]{98}](https://img.qammunity.org/2023/formulas/mathematics/college/jp6r4sak9vwt701jyk16jbyo74dm9qlckl.png)
Therefore
![\sqrt[]{98m^(12)}=m^6\sqrt[]{98}](https://img.qammunity.org/2023/formulas/mathematics/college/a57wf6u999x6hx9lh53thwwqegmxxx3xob.png)
Now we can just factor 98 inside the square root:
Then
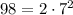
We can put it inside the square root
![\begin{gathered} m^6\, \sqrt[]{98}=m^6\, \sqrt[]{2\cdot7^2} \\ \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gm4wa1419vz22m27nwby6b2a3ezkc108h3.png)
Now we can simplify the square with the square root
![m^6\, \sqrt[]{2\cdot7^2}=7m^6\, \sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/434ouhqhe3pur4dzajn6yulmn4e989q4x3.png)
That's the final result
![\sqrt[]{98m^(12)}=7m^6\, \sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/6grzqt9vjoq2c446u7g95behaqifd6jh3j.png)