Question

Simplify (sqrt)98m^12Using factor tree. Please draw. Quick answer = amazing review. Not a graded or timed assessment

Answer 1

We can directly remove m^12 from the square root, and stay only with 98 inside the square root

`\sqrt[]{98m^(12)}=m^{(12)/(2)}\sqrt[]{98}=m^6\sqrt[]{98}`

Therefore

`\sqrt[]{98m^(12)}=m^6\sqrt[]{98}`

Now we can just factor 98 inside the square root:

Then

`98=2\cdot7^2`

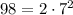
We can put it inside the square root

`\begin{gathered} m^6\, \sqrt[]{98}=m^6\, \sqrt[]{2\cdot7^2} \\ \\ \end{gathered}`

Now we can simplify the square with the square root

`m^6\, \sqrt[]{2\cdot7^2}=7m^6\, \sqrt[]{2}`

That's the final result

`\sqrt[]{98m^(12)}=7m^6\, \sqrt[]{2}`