Question

Identify the sequence below as arithmetic, geometric, or neither. Then find the next two terms.20, -60, 180, - 540,...Choose the correct type of sequence below.arithmeticneithergeometricThe next term in the sequence, as,is(Simplify your answer.)(Simplify your answer.)The next term in the sequence, ag, isClick to select your answer(s).

Answer 1

Given sequence is:'

20 , - 60 , 180 , - 540

Now, for Arithmetic sequence, we must have:

difference between second term and first term = difference between third term and second term and so on for all the terms.

That is, -60-20 = -80 must be equal to 180-(-60) = 240

Clearly,

`-80\\e240`

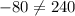
So, the sequence is not arithmetic.

Now to check,

If the sequence is geometric or not,

The ratio of every next term and the previous term must be equal for all the terms,that is,

`\begin{gathered} (-60)/(20)=(180)/(-60)=(-540)/(180) \\ -3=-3=-3 \end{gathered}`

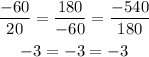
Clearly the ratio is same so the sequence is geometric.

To find the next two terms of the sequence, we will multiply the terms by (-3).

The next two terms will be :

`\begin{gathered} -540*-3=1620 \\ 1620*-3=-4860 \end{gathered}`

Hence, the given sequence is geometric .

The next two terms are 1620 , - 4860